Geometria Sagrada: Dia do PI em 14 de março
Posted by Thoth3126 on 14/03/2018
O DIA DO PI:
Neste sábado 14 de março (3,14, como as datas são feitas em inglês), é o dia do PI. É uma ocasião para celebrar uma das constantes matemáticas mais interessantes e misteriosas da natureza e que é responsável pela criação do universo inteiro.
O número de Pi aparece em equações que descrevem as órbitas dos planetas, , dos sistemas solares, das galáxias, aparece nas cores das auroras boreais, na estrutura do DNA humano, na geometria de um floco de neve, etc. O valor de PI esta tecido na trama da vida, dos planetas, dos sóis/estrelas, do universo e … de tudo o mais.
Tradução, edição e imagens: Thoth3126@protonmail.ch
Geometria Sagrada: Dia do PI é em 14/03, afinal o número PI faz esta data em inglês: 3-14 (3,141592…)
Neste sábado, dia 14 de março de 2015 pode ser escrito 3/14/15 no formato de data dos EUA, que corresponde aos primeiros dígitos de um constante matemática Pi: 3,1415. O melhor momento para desfrutar de toda a “irritabilidade” dos dias de hoje é celebrá-la em 09:26 e 53 segundos, da manhã e depois à noite, quando então a própria passagem do tempo combina com todos os 10 dígitos iniciais do número Pi: 3,141592653.
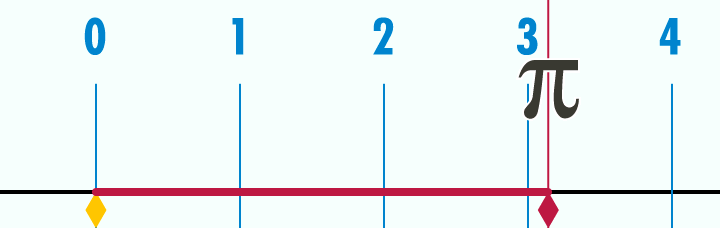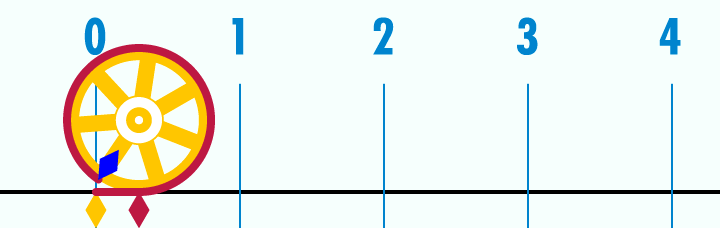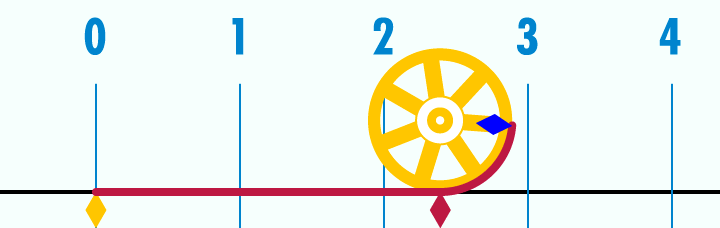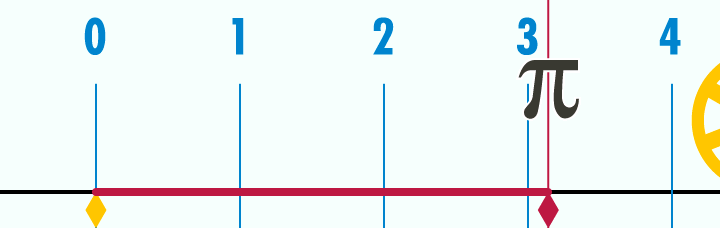
O número Pi π é a relação do diâmetro com a circunferência do círculo.
A data acontece uma vez a cada 100 anos e os verdadeiros fãs de matemática e do Pi devem realmente saborear o momento que só acontecerá de novo em 2115. Para os admiradores da teoria da relatividade geral é também uma ocasião para celebrar o aniversário de Albert Einstein, que também é em 14 de março.
Os seres humanos têm lutado para calcular π nos últimos milhares de anos. Divida a circunferência de um círculo pelo seu diâmetro, essa relação entre os dois números é π, ou seja, não importa o tamanho do círculo, desde uma cabeça de alfinete a um sol gigantesco, o resultado será sempre o mesmo. Este é talvez, o número mais sagrado na geometria sagrada utilizada na construção do universo material.
O seu cálculo parece muito simples, mas o diabo está escondido nos números. Enquanto o valor de π é finito (um pouquinho mais do que 3), o número decimal é infinitamente longo:
3,1415926535897932384626433832795
02884197169399375105820974944592307
81640628620899862803482534211706… mais
Supercomputadores conseguiram calcular mais de 2,7 bilhões de dígitos após a vírgula e eles ainda estão triturando chips buscando por mais números.

Os antigos babilônios já tinham o conhecimento da existência de π – a proporção entre a circunferência com o diâmetro em qualquer círculo. A constante obtida foi de 3.125, fazendo uso de seu conhecimento de que o perímetro de um hexágono regular inscrito em um círculo é igual a seis vezes o raio do círculo.
Ao utilizar este perímetro do hexágono inscrito como um limite inferior para a circunferência do círculo, eles foram capazes de chegar a um resultado notavelmente próximo do valor de π por volta de 2.000 a.C.
Durante o século V a.C, Hípias de Elis descobriu o quadratrix, uma curva que pode ser usada para determinar π através de uma construção geométrica. A quadratrix de Hípias’, poderia ser usada para a “quadratura do círculo”, embora não de uma forma aceitável para os geômetras da antiga Grécia ( ou mesmo para os modernos).
A “Quadratura do círculo”, foi o problema colocado pelos antigos gregos, em que um quadrado deveria ser construído com sua área igual à de um determinado círculo. No século III a.C, Arquimedes de Siracusa, amplamente aceito como a maior mente científica da Antiguidade, descobriu um método pelo qual π pode ser determinado com qualquer grau de precisão desejado.
O resultado de PI, O Cosmos…
Este método de Arquimedes para calcular π em polígonos regulares inscritos e circunscritos em torno do círculo. Sua concepção do uso de limites superiores e inferiores atingiram o limite do cálculo diferencial. O valor de Arquimedes foi de π = 3 10/71 < π <3 1/7.
No século V d.C na China, o matemático Tsu Chung-Chi estabeleceu que o valor de PI era 3.1415926 < π <3.1415927 uma precisão que não foi alcançada na Europa até o século XVI. Os chineses, assim como Arquimedes poderiam calcular o valor de π a qualquer grau de precisão desejado.
O rearranjo de um círculo
Leonardo da Vinci (no século XVI) e um documento japonês do século XVII encontraram a área aproximada de um círculo pelo seu rearranjo. Este método divide o círculo em setores iguais e os organiza em um paralelogramo aproximado. Este método não é sofisticado, por isso suspeita-se que uma forma deste método foi usada por povos antigos para encontrar a área de um círculo.
A descoberta de representações em séries infinitas para π pelos matemáticos como Gregory, Leibniz e Euler no século XVII e XVIII, tornou possível calcular dezenas de dígitos com relativa facilidade. Em 1666 Newton tinha encontrado uma maneira de calcular π, usando o teorema binomial, a 16 casas decimais, utilizando apenas 22 termos de uma expansão de série infinita.
A quadratura do círculo é um problema proposto pelos antigos geômetras gregos consistindo em construir um quadrado com a mesma área de um dado círculo servindo-se somente de uma régua e um compasso em um número finito de etapas.
Em 1882, o matemático alemão, F. Lindemann provou que o número π e sua raiz quadrada eram números transcendentais, aqueles que não podem ser raízes de equações polinomiais com coeficientes inteiros. A descoberta de Lindemann resolveu o problema da quadratura do círculo colocada pelos gregos mostrando que é impossível o cálculo usando régua e compasso e as regras dos antigos geômetras gregos.
Hoje em dia é fácil de obter mais dígitos do número π que são realmente úteis. O que antes era difícil aproximar-se de três ou quatro dígitos é agora trivial para um computador calcular até centenas de milhares de dígitos. No entanto, a computação de muitos dígitos π é um bom teste de velocidade e precisão de um computador. O cálculo do valor aproximado de π já esta em 100.000 dígitos.
Modos muito estranhos para calcular π podem ser vistos hoje: lançar agulhas em uma mesa ou cachorros-quentes congelados no chão. É Hora da festa!
Para mais informações, leitura adicional:
Permitida a reprodução, desde que mantido no formato original e mencione as fontes.







Nenhum comentário:
Postar um comentário